B+ 树
B+ 树是最常用的索引数据结构,在数据库中被广泛应用。也是数据库索引常考的知识点。
1. B+ 树简介
1.1 B+ 树的特点
- B+ 树是一种特殊的平衡树,通常用于数据库和文件系统中
- B+ 树的每个节点最多有
M个子节点,M是 B+ 树的阶数 - 区别于其他平衡树,B+ 树最重要的特点就是:所有的数据只存储在叶子节点中
- 每个叶子节点都有指向兄弟节点的指针,所有叶子节点组成了一个有序链表,便于进行范围查询
下图为一个 3 阶的 B+ 树:
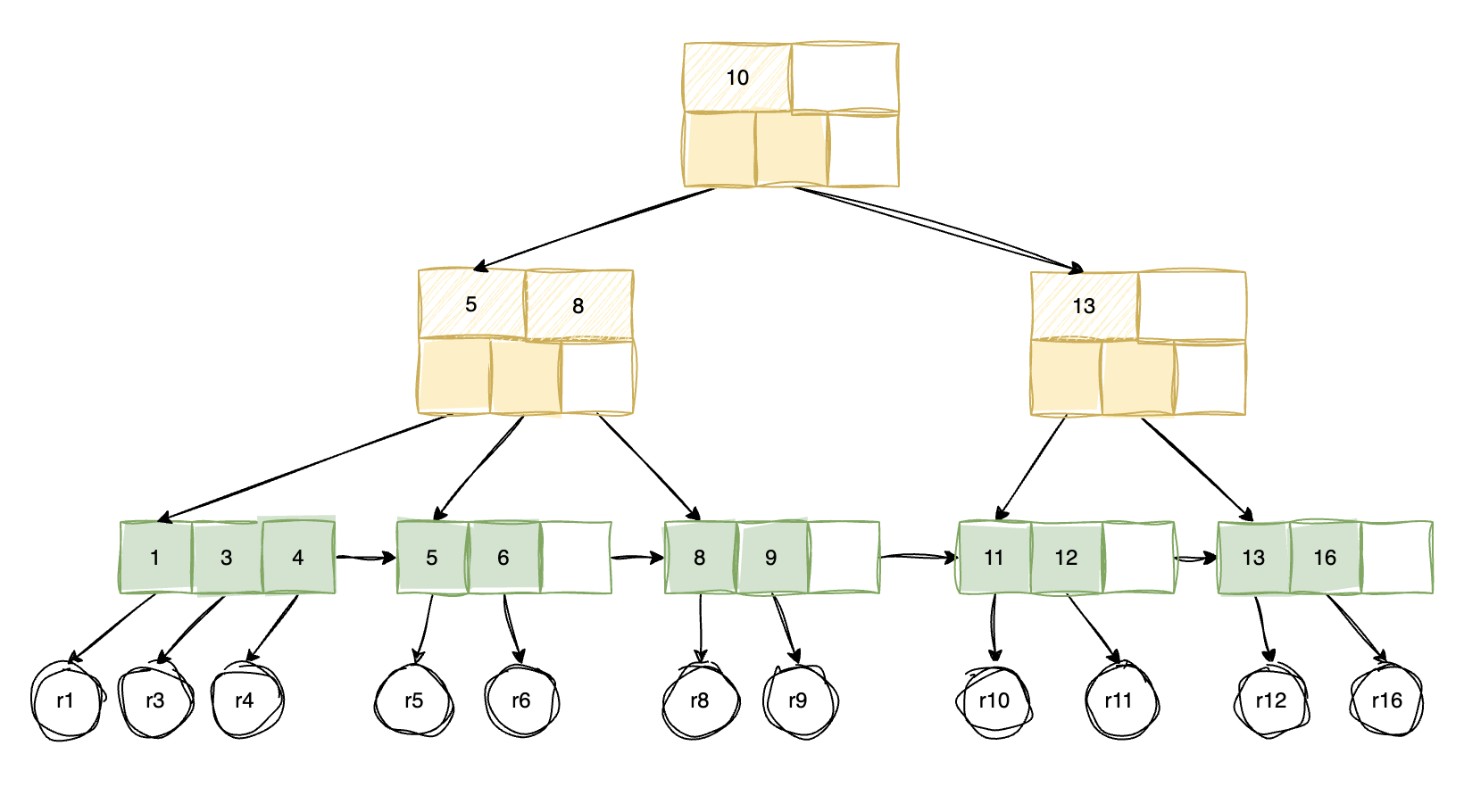
1.2 与 B 树的区别
B+ 树是对 B 树的一种优化。二者的核心区别如下:
- B+ 树只在叶子节点存储数据,而 B 树所有的节点都会存储数据
- B+ 树的叶子节点之间有指针,组成了一个链表,便于进行范围查询
从上面的区别也可以推导出二者在查询和存储上的性能区别:
- B+ 树会占用更多的存储空间:B+ 树只有叶子节点保存数据,相比 B 树,会多出许多用于索引的中间节点
- B+ 树范围查询更快:B+ 树的叶子节点组成了一个有序链表,在找到范围的起点后,可以快速找到范围的终点
- B+ 树单点查询稍慢一下:因为 B 树每一个节点都保存了数据,所以在遍历时,查询到指定节点会立即结束查询。而 B+ 树一定要遍历到叶子节点才能结束查询
2. B+ 树的结构
2.1. 节点种类
我们可以将 B+ 树的节点分为三类:
- 叶子节点:在 B+ 树的最底层,存储实际的数据
- 中间节点:存储子节点的索引,用于快速定位数据
- 根节点:一种比较特殊的节点。通常是一个中间节点。如果 B+ 树此时只有一个节点,那么根节点同时也是叶子节点
2.2. 节点结构
与普通树的节点结构类似,只是 B+ 树中会稍微区分一下中间节点与叶子节点的结构。
对于中间节点来说,需要保存子节点的索引,以及指向子节点的指针。
class InternalNode extends Node {
private boolean isLeaf; // 是否是叶子节点
private List<Node> keys; // 保存子节点的索引
}
而叶子��节点则需要保存数据,以及指向兄弟节点的指针。
class LeafNode extends Node {
private boolean isLeaf; // 是否是叶子节点
private List<T> data; // 保存数据
private LeafNode next; // 指向兄弟节点的指针
}
2.3. 节点与 Keys 的数量
M 是 B+ 树的阶数,表示每个节点最多有 M 个子节点,这里还有另一层含义。
每一个子节点都索引了一段数据,每向下一层,这一段数据又会被拆分成最多 M 个子分段。
将一段数据切分为 M 个子分段,需要 M-1 个索引。所以,每个中间节点,Keys 的数量最多为 M-1。
3. B+ 树的常见操作
3.1. 单点查询
先来看一下最简单的单记录的查询。与使用搜索树查询的流程一致:
- 从
Root节点开始,遍历所有的Keys,找到待查询的Key所在的子节点 - 重复这一个过程,直到遍历到叶子节点
- 搜索叶子节点中的数据,查询是否有对应的记录。这一步可以使用 二分查找 来优化
3.2. 范围查询
范围查询的流程与单点查询类似,只是多了一个遍历到终点的步骤。
- 根据单点查询的流程,找到范围的起点
- 从起点开始,沿着叶子节点顺序遍历,直到范围的终点。这期间的数据就是范围查询的结果
因为叶子节点之间有指针,所以遍历的过程是线性的。只会在查询起点时对树进行搜索。
常见考点:为什么叶子节点要连成链表?
因为在范围查询中,经常要跨多个叶子节点查询数据,如果叶子节点之间没有指针,那么需要重新搜索树,才能够找到下一段数据的起点。
3.3. 插入
相比于查询,插入与删除操作要麻烦一些,因为会涉及到树的「再平衡」。
B+ 树要求每个节点的 Keys 数量在 [M - 1/2, M] 之间。一旦超出了这个范围,就需要进行再平衡。
- 基于范围查询的步骤,找到需要插入新的数据的叶子节点
- 如果插入后,节点的
Keys数量在[M - 1/2, M]之间,则直接插入 - 如果插入后,节点的
Keys数量超过了M,则需要重新平衡 B+ 树 - 将当前节点分裂为两个节点,保证每个节点的
Keys数量在[M - 1/2, M]之间 - 将分离后的右侧的节点的
Key值插入到父节点中 - 需要注意的是,在父节点插入
Key值后,可能会导致父节点也超出Keys数量范围,需要继续递归分裂父节点 - 如果直到
Root节点也超出了Keys数量范围,则Root节点也需要分裂,此时需要创建一个新的Root节点,树的高度增加一层
3.4. 删除
删除操作的流程与插入操作类似,只是将节点的分裂操作改为合并操作,并且多了一个「借」的操作。
- 基于范围查询的步骤,找到需要删除的数据的叶子节点
- 如果删除后,节点的
Keys数量在[M - 1/2, M]之间,则直接删除 - 如果删除后,节点的
Keys数量低于M - 1/2,则需要重新平衡 B+ 树 - 重新平衡的时候,首先会尝试向兄弟节点「借」一个
Key值,如果兄弟节点有多于的Key值(也就是借出一个节点后,依然满足Keys数量范围),则直接借一个过来,然后调整父节点中的Keys值 - 如果兄弟节点都无法借出,则需要将当前节点与兄弟节点合并,并且对应地减少父节点中
Keys的数量 - 仍然要注意,减少父节点的
Keys数量后,可能会导致父节点也超出Keys数量范围,需要继续递归调整父节点 - 如果递归调整到
Root节点,Keys的数量只有一个,也就是刚刚合并后的子节点,那么删除掉现有的Root节点,将合并后的子节点作为新的Root节点,树的高度减少一层
「借出」的操作是删除流程中一个小优化。因为如果借出操作成功,那么不会影响到父节点的 Keys 数量,所以不需要继续递归调整父节点。
3.5. 再平衡的要点
再平衡的要点就是:
- 保证节点的
Keys数量在[M - 1/2, M]之间,不论是超出或者低于,一旦节点Keys数量不满足条件,就需要进行再平衡 - 再平衡过程中,可能会导致父节点的
Keys数量也不满足条件,需要继续递归分裂父节点 - 如果递归的节点是
Root节点,Keys的数量依然不满足条件,则要根据情况创建新的Root节点,或者合并已有的节点成为新的Root节点,此时会导致树的高度变化
4. 常见考点
- B+ 树的特点是什么,与 B 树的区别是什么
- 为什么 B+ 树的叶子节点要连成链表
- B+ 树的查询、插入、删除操作的流程是什么